競争社会での最適行動
今回は、数学から生まれた経済学分野の『ゲーム理論』に触れてみたい。ゲーム理論は、ビジネスの世界でも活用されることの多い実践的な学問だ。
私たちは1人で生きているわけではなく、味方や敵に囲まれて生活している。社会の中で自分はいかに行動すべきかを考えることを想定してみよう。例えば、誰と結婚するか、子供をどう教育するか、新規事業を上司にいかに認めさせるか、会社をいかに経営するかなど重大な決断をする状況において、多くの場合、自分1人だけで決定するわけではない。自分の決定は、周囲の人の決定とかかわっているといえる。
この「自分の決定は外部の決定とかかわっている」ことを理解するために、以下の2つのケースを考えてみる。
新規事業提案での行動
新規事業を上司に認めさせる時、自らが企画したA案、B案の2つのプランを持っており、A案はリスク度が30、B案がリスク度が15、その他の諸条件は同じと仮定しよう。
自分としては、できればA案を採用して欲しいと思っているが、上司は非常にリスクを嫌う人物だ。自らが企画したA案、B案のどちらも採用されなければ自分の評価は下がってしまいかねない。このような場合どうすればいいだろうか。
A案、B案の2つの案を上司に提案すれば上司はリスク度の少ないB案を選ぶことが推測できる。自分はA案に大変魅力を感じておりA案のみを提案したいが、A案のみを提案してA案が採用されなければ自分にとってマイナス評価がつくことも推測できる。
自分にとってプラスの選択とは、どのような案であっても採用されることが最優先になるので「上司がB案ならば採用するであろう」との合理的推測によってB案を提案することに決定せざるを得ない。
このように自分の決断は自分1人で決めたものだが、実は上司が決断するであろう結果に影響を受けていることが分かる。「自分の決定は外部(上司)の決定とかかわっている」ことになる。
もう一歩進めて考えると、A案(リスク度30)よりリスクのあるC案(リスク度40)を作成し、上司にA案かC案を選んでもらえばA案が通るかもしれない。しかし、上司がリスク度30以上の案を全く受け入れない人であれば、A案、C案ともに受け入れられない最悪の事態になってしまう。
仮に、新規事業の提案が3カ月に1度、年間4回あるなら、4回に3回は上司の推すであろう案を用意するとか、上司の意見を取り入れた案を作成するなど上司の機嫌をとる作戦をとる。そして、4回に1回は上司をまったく無視して自らが思った案を主張しても上司は「3回は私の意見を汲んでくれているから、1回は好きなようにやらせてみるか」と思うかもしれない。「自分の決定は外部(上司)の決定とかかわっている」ことになっている。
市場独占状態での戦略
A社がある市場を独占しており、この市場はまだまだ成長が見込めるとしよう。
A社は自社に与えられた資源を有効に利用して、最大限の利益を追求することにのみ注力するだろう。これだけであれば話は非常に簡単だが、まだまだ成長が見込める市場にまったくライバルが出現しないことはありえない。ライバル出現の可能性に備えて、A社は以下のような自社のとるべき行動を考えるだろう。
- A社はライバル企業の出現をできる限り遅らせる
- ライバル会社が出現した場合、A社の利益を何とか確保する
- A社のシェア確保の施策を考える
これがいわゆる企業戦略というやつだ。ここでも「自分(A社)の決定は外部(ライバル)の決定とかかわっている」ことになる。 そして、競争社会での最適行動を考える理論がゲーム理論なのだ。
ゲーム理論では、互いの目的達成のために完全に敵対するケース、協力するケース、敵対するが、ある部分においては協力関係にあるといったような複雑な関係も出現する。当コラムでは、なるべくシンプルなケースを記述したい。
ゲーム理論「囚人のジレンマ」
ゲーム理論における題材の最も有名なものに「囚人のジレンマ」というものがある。
囚人のジレンマ
ある事件で、共犯であることが確実な容疑者AとBが別件で逮捕され、別々の部屋で事情聴取を受けている。刑罰については2人とも黙秘すればこの事件は立証されず、それぞれ別件での2年懲役となる。1人が本件を自白してもう1人が黙秘した場合は、黙秘した側は懲罰的に10年の懲役で、自白した本人は減刑で1年の懲役、かといって2人とも自白してしまうと2人とも5年の懲役。この場合、容疑者のとる行動は、以下の4パターンが考えられる。
- A、Bが黙秘:ABとも2年懲役
- A、Bが自白:ABとも5年懲役
- Aが自白しBが黙秘:Aは1年懲役、Bは10年懲役
- Bが自白しAが黙秘:Bは1年懲役、Aは10年懲役
どのように行動すれば自分にとって最もプラスの状況になるだろうか。まず、上記の状況を図にして考えてみよう。
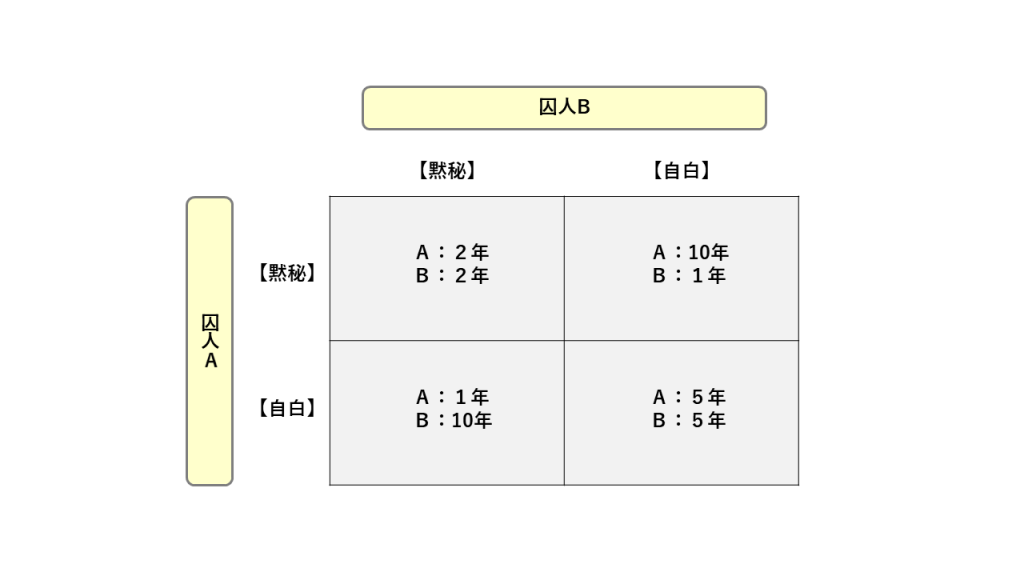
囚人Aについて考えてみる。囚人Aにとって最も都合の良いパターンは、囚人Bが黙秘している時に自分が自白するパターンだが、囚人Bにとっても、その事情は同じなので、相手が黙秘することは期待できない。次に自分1人が黙秘することを考えたとしても、囚人Bが自白すれば自分にとって最悪の状態になってしまう。
囚人Bにとっても状況はまったく同じ。従って、囚人A、囚人Bともに最悪の状況を避けるために自白することになる可能性が非常に高い。ゲーム理論においてはこのような互いに妥協できる状態を「均衡点」という。人は最悪の状況だけは避けられたものの、2人にとってより良い状態である懲役2年(互いに黙秘)という結果は得られない。
ここに「囚人のジレンマ」の問題点が潜んでいる。2人のとった行動は、十分に合理的なものといえるが、なぜ2人にとって最良の結果にならなかったのだろうか?
ひとつは囚人A、囚人Bが「協力できなかった」ことが最大の原因だ。このようなケースをゲーム理論においては非協力型ゲームという。現実の非協力型ゲームには、先物市場のようなゼロサムゲームから囲碁・将棋のような対戦・同時進行ゲームなどがある。
もうひとつは「人は考えられる最悪の選択(絶対劣位の戦略)は排除して行動をする」ところにある。囚人のジレンマのようなケースを実際の経済活動に置き換えて考えてみよう。
競合する駅前弁当店
ある都市の駅前では弁当店が通りに面して向かい合っており、サービス・品質・価格ともに差がないとしよう。月間利益がA店は600万円、B店が400万円とする。この利益の差は単純に立地条件だけでついた差であろうと推測できる。
そこで、B店は何とかして現在より利益を増やそうと考えた時、向かい側のA店の顧客を奪い、集客アップを図ることを第一に考えるだろう。その際にB店がとるべき戦略として、サービスの向上、品質の向上、価格値上げ、価格値下げの4つの選択肢があるとする。さて、どの戦略を選択すればよいだろうか。
B店の経営者は次のように考えるだろう。「サービスや品質の向上には人手や新しい設備がかかるし、価格値上げは集客をダウンさせてしまう。一番簡単な方法は価格を値下げをして集客をアップさせ、売り上げを増やせばよい」と。そこで、B店の経営者はある市場調査会社に「価格を20%ダウンさせた場合の当社の集客状況、売り上げ、利益をシミュレーションしてくれ」と依頼した。
依頼を受けた市場調査会社は次のような結論を出してきた。
- B店が価格を20%下げれば、飛躍的に集客・売り上げともにアップし、月間の利益は約560万円になり、この時のA店の利益は約300万円と半減する
- 逆にA店が先に価格値下げ戦略に出てきたら、A店の利益は740万円に上昇し、B店の利益は200万円まで下がる
先手を打って価格値下げ戦略をA店より先に実行に移す方が得策という結論をその市場調査会社が出してきたが、この案は正しいだろうか?
まず、下図を使って A店、B店の利益について考えてみよう。
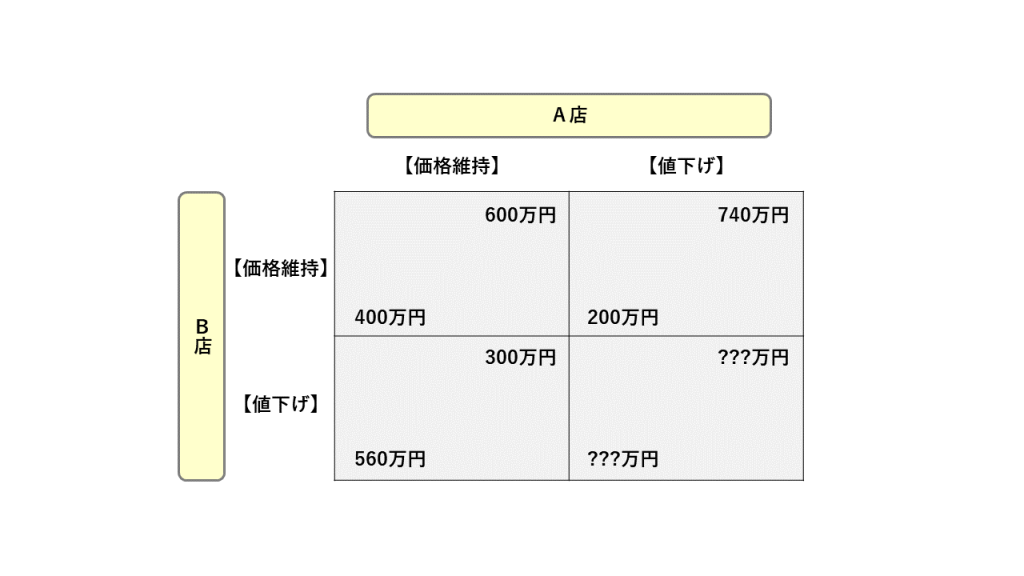
市場調査会社の提案はある意味では正しいといえるだろう。先に価格値下げを実行したB店は集客・売り上げともにアップすることは明白だ。しかし、もう一歩掘り下げて、集客・売り上げともにダウンし、利益が激減したA店はどうするか考えてみよう。
合理的に推測すれば、A店が何もしないはずがなく、1~2カ月の内に必ず反撃にでてくることが予想される。その際A店にとって最も手っ取り早い反撃方法といえば、「価格値下げ戦略」といえるだろう。
A店は、B店と同じ価格に値下げするだけで、B店に奪われた顧客を取り戻せる。そして、A店はB店と同じ価格に値下げしてきた。その結果を図でみてみよう。
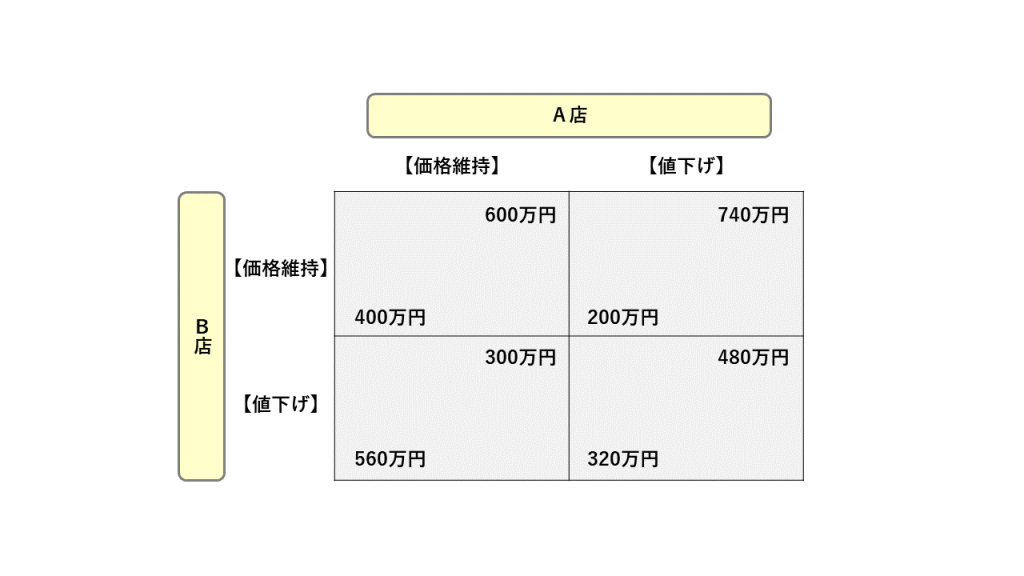
結果は、集客数はB店が値下げする以前の状態に戻り、従って、A店B店ともに集客数は変わらないまま、客単価が下がったために売り上げが減少し、B店の月間利益が320万円、A店の月間利益が480万円と互いに利益を失うことになった。
もし、このまま価格競争を続けるとすればどうなるだろう。どちらかの店がつぶれるまで続けることになりかねない。このような価格競争が激化して倒産というようなことになれば、「囚人のジレンマ」のような非協力型ゲームにみられる最悪の選択より悪い状態に陥ってしまう可能性がある。この場合の最悪の選択は相手が値下げしたにもかかわらず、自分が何の対抗手段を講じないで利益を大幅に減らすことだ。
従って、合理的な推測から、このような結果がともなわない状態が予想される場合「人は考えられる最悪の選択は排除して行動をする」ため価格競争は1度でやめることになる。この「価格競争は1度でやめる」状態が、囚人のジレンマでみられる均衡点に該当する。この状態では、互いに利益は減っている。
ここで再び合理的な推測をしてみよう。
1度の価格競争によってB店の月間利益は「400万円→560万円→320万円」と推移することになる。
月間利益が560万円の期間が2カ月とした場合、「( 560万円-400万円)×2=320万円」の利益増加が見込めますが、次段階の月間利益320万円が続いた場合には、「320万円÷( 400万円-320万円)=4カ月」で、その利益増加分が消えてしまう。
これを年間利益で考えてみると、「400万円×12カ月=4800万円」から「560万円×2カ月+320万円×10カ月=4320万円」に減ることになる。従って、恒常的な価格競争に陥り、大きく利益を失うことになるかもしれない戦略は1度でもすべきでないという結論を導き出すことができる。
以上のことを踏まえて、B店の経営者はこんなことを考えた。
「恒常的な価格競争はB店の体力がもたない。恒常的な値下げは1度でも行うと利益はいずれ減る。では期間限定ならどうだろうか? もし1カ月間限定で値下げすれば、その1カ月間の利益は、400万円から560万円にアップし1カ月後には元の価格に戻せば利益は400万円確保できる。それならば半年に1回、いや3カ月に1回の割合で期間限定値下げを行えば、年間利益は大幅にアップするはずだ。」
この「期間限定値下げ」の考え方が正しいか否かを合理的な推測のもとに判断してみよう。
まず、B店の利益アップはA店の顧客を奪うことによって初めて可能となることが前提だ。では、顧客を奪われたA店はどのような対抗策をとるだろうか。
考えられる対抗策は、B店と同じ期間の「期間限定値下げ」だ。A店にとって、B店がある日突然行う第1回目の「期間限定値下げ」はまさしく晴天の霹靂。当然A店はその値下げに対して準備ができていない。しかし、日に日に減る売り上げに焦り、2週間後には「期間限定値下げ」を行うかもしれない。
B店の2回目の「期間限定値下げ」の際には、第1回目の経験から既に準備ができているため、B店の値下げ開始日の翌日にはA店も値下げを開始できるだろう。B店が考えることはA店も同じように考えるとすれば、いずれB店が値下げを開始する日を推測し、B店値下げ開始日の1日前にA店が値下げを開始するといった状況になるだろう。従って、B店経営者の考えた「期間限定値下げ」も有効な戦略とはいえない。
互いに値下げを恒常的に続けると利益が減ることは明白なので、値下げは期間内に終わると考えられるが、「相手側が終わるまで、こちらも終われない。また、できれば、相手が値下げを中止してからさらに1カ月間値下げを継続できれば自分の利益が増える」と考えた場合、互いに値下げを中止できずに利益を失うことになる。
以上のことから、恒常的なものであれ、期間限定であれ「値下げ戦略」はB店にとって良い選択でないことが分かった。何としてもA店の顧客を奪いたいでのであれば、サービスや品質の向上で差異化を図るほうがよいだろうし、あるいは、A店の顧客を奪うことなく、売り上げは現状のままで、コストダウンを図ることによって月間利益のアップを狙ったほうがよいということになる。
もし、値下げをするのであれば、こちら側からではなくA店が値下げを行った時のみ、防衛の意味で値下げするにとどめるのが得策といえる。
しかし、周りを見渡すと、現実の経済活動では、国道沿いに並んでいるガソリンスタンドが乱売合戦をしたり、ハンバーガーショップが値下げ競争をしたり、このほかにもスーパーマーケット、家電量販店など多くの店が同様のジレンマに陥っている。
今回の例のA店、B店は、現状のまま店を経営すれば両店合わせて1000万円の利益が上がっている。しかし、A店、B店が値下げ戦略を採った場合、両店合わせての利益が1000万円から800万円へと減っている。この差額の200万円の意味するところは一体何か。
実は、この両店の利益喪失分が消費者の利益となっているのだ。今回の例では、社会全体をA店、B店、消費者の3者とみることができる。社会全体からみれば、A店、B店の値下げ競争により、消費者が利益を享受していることになるのだ。仮に「値下げ戦略」では相手を出し抜けないと分かると「サービス・品質の向上戦略」などを用い、競争状態に入るのが一般的だ。
このような競争の結果起きる価格の低下やサービス・品質の向上が、最終的には消費者の利益になっている。
競争状態での戦略
今回はゲーム理論における戦略の考え方を簡単なケースを基に紹介した。ただし、ゲーム理論における多岐にわたる考え方のすべてを紹介したわけではなく、最も基礎的な考え方を示しただけだ。最後に、競争状態における戦略の基礎的な考え方をまとめておこう。
■先を読んで、合理的に今を推測しよう
自分の最初の意思決定により相手がどのように対応してくるか、また、それに対して自分の最善の選択を推定する必要がある。
■絶対優位の戦略がある時はそれを用いよう
相手がどのような対応をしてきたとしても、自分にとって絶対優位の戦略があるとするならば、その戦略を用いればよい。ただし、すべてのケースにおいて「絶対優位な戦略がある場合は稀である」ことは常に念頭に入れておいたほうがよい。
■絶対劣位の戦略を考慮から外したうえでさらに考察を進めよう
絶対劣位の戦略は相手の戦略とは無関係にどの選択にも劣る戦略といえる。従って、絶対劣位の戦略を自分が持っていれば、その戦略は外して考えるべきであり、相手が持っているとするならば、その戦略は選ばないと予測することができる。
また、二者択一の場合、一方が絶対劣位の戦略だとするならば、もう一方を選択することは容易に推測できる。
駅前弁当店の例で、B店の値下げ戦略に対抗するためにはA店は値下げをし、互いに利益は減るものの均衡点を選ぶしか方法はなかった。A店にとってB店の値下げ戦略に何の対抗策も打ち出さず、傍観するのは自社の利益が激減するだけの絶対劣位の戦略といえる。しかし、同時に絶対優位の戦略も用意されていないことも事実だ。
■絶対劣位の戦略を消去したうえで、絶対優位の戦略を見つけようとしても解決に至らない場合には、均衡点を探そう



